Sistema de Inecuaciones con dos Valor Absoluto, resolución
CLICK EN EL VIDEO PARA LOS EJERCICIOS
Un sistema de inecuaciones se identifica porque las inecuaciones se encuentran entre llaves, esto indica que la solución debe ser la intersección de los conjuntos de las inecuaciones que conforman el sistema.
Luego, si la inecuaciones son con valor absoluto, se busca la solución de cada inecuación, bien sea intersección, si el signo de la desigualdad es «<«, o unión si el signo de la desigualdad es «>», para luego hacer la intersección de estos conjuntos y así encontrar la solución del sistema.
Es importante destacar que cuando se tiene un Sistema se busca encontrar el punto (en el caso de sistema de ecuaciones) y el conjunto de puntos (área en el caso de sistema de inecuaciones) que satisfacen a las dos o tres inecuaciones.
Entonces un sistema de inecuaciones puede estar conformado por dos o más inecuaciones. Hay profesores que enseñan a los muchachos a trabajar las dos o tres al mismo tiempo, manteniendo la llave al lado izquierdo.
Particularmente me gusta desarrollar cada inecuación por separado hasta llegar a la solución gráfica, el intervalo y el conjunto, para luego comenzar con el resto.
Trato de enseñar al alumno una estructura que le permita identificar cualquier error y poder corregirlo rápidamente.
A continuación se presenta un ejercicio resuelto, es un sistema de inecuaciones con valor absoluto. En el VIDEO también explico el ejercicio.
En las siguientes figuras se explica un sistema de inecuaciones, donde las inecuaciones tienen valor absoluto.
Figura Nº1. Se resuelve la inecuación uno
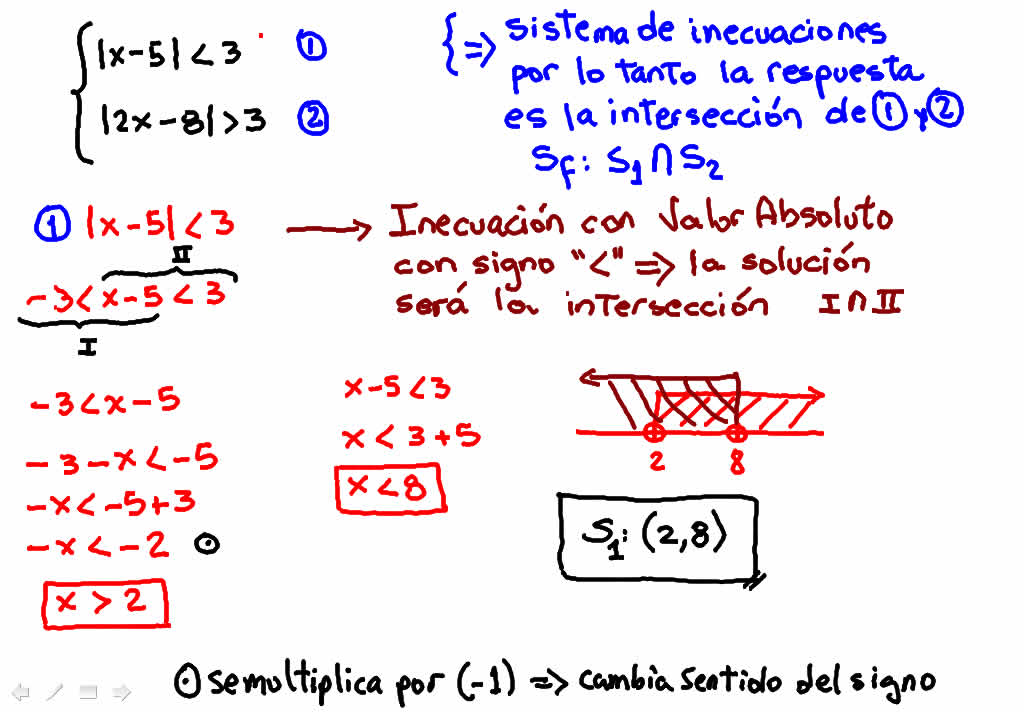
Como podrás observar desarrolle la inecuación UNO para poder determinar el conjunto de valores que satisface dicha inecuación.
En la siguiente figura se resuelve la inecuación dos para luego encontrar la solución del sistema como la intersección de ambas.
figura Nº 2. Se resuelve la inecuación dos y la solución final
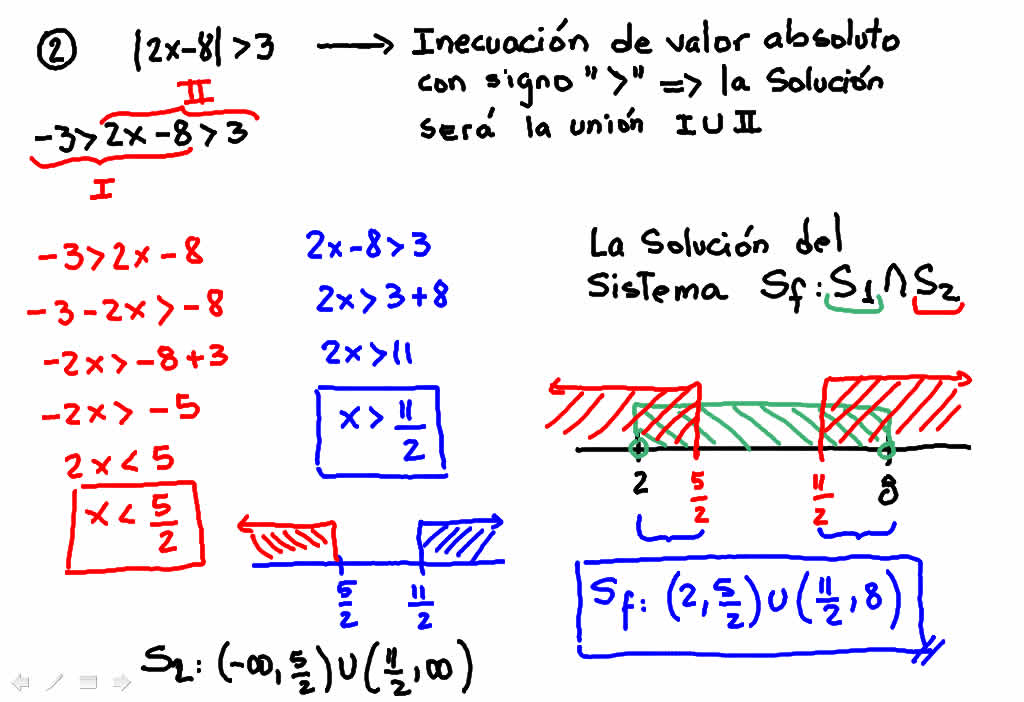
Las soluciones se pueden representar de tres o cuatro formas: la analítica: que es la que se determina cuando resolvemos cada inecuación. El intervalo: expresado entre corchetes o paréntesis. Solución gráfica cuando la representamos en una recta real y por último la representación en conjunto.



Buenas, continua dando clases por skype?
te amo
Gracias Joel. El blog esta en proceso de remodelación, en cuanto se termine se seguirá agregando artículos, mantente en secuencia.
muy bueno su artículo, de verdad me gustó, muy didáctico y preciso, saludos.
Hola Elizabeth, es importante tener claro algunos conceptos, como por ejemplo Valor Absoluto. Recuerda que esta función genera dos funciones en intervalos distintos. Para resolver esta ecuación hay que tomar |2x-5| y expresarlo como 2x-5 si 2x-5>0 y será -(2x-5) si 2x-5<0. Se aplica la misma definición para |x| y podrás ver que obtendrás como 4 ecuaciones.
Que tal Profesora!
Muy interesantes y de gran ayuda sus artìculos. Tengo problemas para resolver la siguiente igualdad x+|2x-5|=1+|x| me podrìa asesorar con los pasos para su soluciòn o algun ejemplo parecido. Gracias!
hermoso
Hola profe quiero agradecer por la labor que haces, ya que nos ayudas muchisimo con las explicaciones.
tengo el siguiente sistema
abs((2x-5)/(2x-1)) menor a 4.
abs(((9x-5)/(4x+3) -2) mayor o igual a 3/2.
abs(3x-5) mayor o igual a 1.
necesito ayuda para la resolucion????
muchas gracias me a servido mucho recordar materia para calculo desde tu pag
hola profe grasias por su ayuda aunk eso lo entiendo pero en otros ejercisios cambia mucho los fatores tendria que ver unos ejercisios de esta categoria pero un poco solo un poco mas fuertes
Hola, si aun funciona, estaba en mantenimiento cambiando de hosting pero ya estoy lista para prestar nuevamente los servicios de clases on line. Para tener clases on line puedes hacer clic en el botón de donación, aportas 7 dolares y me estare comunicando conitgo para darte clases por skype
Hey esta pagina aun funciona..?? es decir aun explicas on line..? Quisiera saber más sobre inecuaciiones del valor absoluto. Pero es YA!. Y cuanto es.
muchas gracias!!! Dios la cuide y la bendigue
como se realizan las inecuaciones liniales y cuadraticas
profe si paso el certamen lunes… viajo y me caso con usted mil gracias
urgente porfis ese ejerciciooo
|x2-9| – 4|x-1| < 3 – x2
Esther lo que hace usted no tiene precio, se agradece muchísimo su labor ya que se aprende muchísimo con sus vídeos.
profe como puedo contactarme con usted
hola soy ernesto quisiera saber como resolver esta inecuación
4x+3 sobre 5x-2 mayor igual que 1 se lo agradeseria
Hola Kathy, especifica que enlaces estan rotos para verificar,
estaba tratando de ver los otros videos porque estoy muy complicada con unos ejecicios…pero el enlace esta roto
Lorena en la expresion que escribes falta el simbolo de desigualdad
Hola soy Lorena Cabrera Soriano y me gustaria que por favor resuelva este ejercicio y me lo pueda explicar de la manera màs fàcil..
2|x-3|^(2)+|7x-21|-15 .. me lo podria mandar a mi correo lorenacs12@hotmail.com la solución..gracias
Victor en la parte inferior de la pagina principal del blog encuentras varios cursos de inecuaciones
hola soy nuevo en la lic en matematicas y estamos viendo inecuaciones y se me hacen muy conplicadas estas cuentas podias ayudarme ya q es muy inportatnte para mi estas materia : estos son los ejercicios que no entiendo:
(ejercicio 1):-5<4x+10
agrasere mucho su apoyo
como resulevo el siguente problema, si un numero se incrementa en 5 el resultado es menor o igual a 5
Gracias, siempre buscando la forma de que aprendan a veces con mucho detalles pero es para todos los niveles
Gracias.
Me encanta tu forma de explicar. =D
Suerte!.
De nada, estoy para ayudar.
muchas gracias