Cómo Resolver una Inecuación Racional estudiando las raíces
Una inecuación racional, es una inecuación formada por fracciones donde el numerador y el denominador son polinomios. Para encontrar la solución de este tipo de inecuaciones, se debe realizar operaciones algebraicas que ubiquen a la variable en un lado de la desigualdad y en el otro el cero.
Una vez encontrada una fracción comparada con cero, se estudian las raíces de los polinomios que conforman el numerador y el denominador.
Se representan en una recta real y se estudian los signos que determinan el comportamiento de la función racional.
Se cumple que al encontrar un intervalo positivo el siguiente será un intervalo negativo, para comprar selecciona un número evalúa la función.
QUE CONOCIMIENTOS SON NECESARIOS?
Cuando estoy enseñando este tema, es importante resultarle al alumno que se exige un nivel de conocimientos alto, que represente la madurez de un alumno de 5to año de bachillerato, ya rumbo a la universidad.
El alumno debe estar consciente que se aplica conocimientos desde el 2do año de Educación Media General, debe recordar y aplicar la factorización, los productos notables.
Combinándolo con el nuevo conocimiento como lo es la Regla de Ruffini, la cual se estudia en el último año de Educación Media General.
Una vez que el alumno domine los conceptos y procedimientos podrá realizar cualquier ejercicio. Es vital que el alumno entienda que la rapidez es importante en el momento de desarrollar un ejercicio, ya que se está preparando para presentar pruebas de admisión para la universidad.
La solución de una inecuación esta representada de tres formas: de manera gráfica cuando se representa las raíces en la recta real, de forma de intervalo cuando se coloca los valores que satisfacen a la inecuación entre signo de parentesis y corchetes, y de manera de conjuntos.
Una inecuación racional puede contener expresiones en el denominador y en el numerador, que sean polinomios de primer grado hasta polinomios de 6 grado o más, una de los procesos para resolver es racionalizar ambos denominadores, es decir buscar las raíces del polinomio..
Los coeficientes de los términos de los polinomios pueden ser números enteros o fracciones, el alumno no debe temer trabajar con ninguno de los valor numéricos que representan a los coeficientes.
Figura Nº1. Operaciones para cambiar de miembro la variable y compararla con cero.
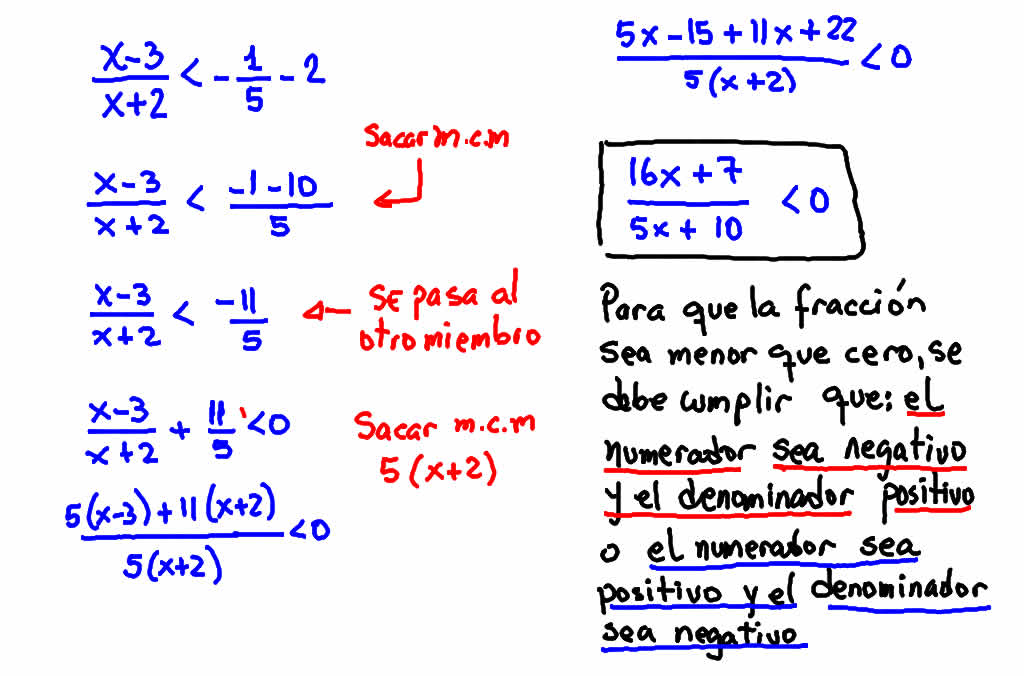
En la primera figura se observa el procedimiento típico de operaciones con fracciones, son conceptos que el alumno trabaja desde su primer año, obtener el mínimo común múltiplo, cambiar términos al otro miembro, realizar distributivas.
Figura Nº 2. Análisis de los valores en la recta real.
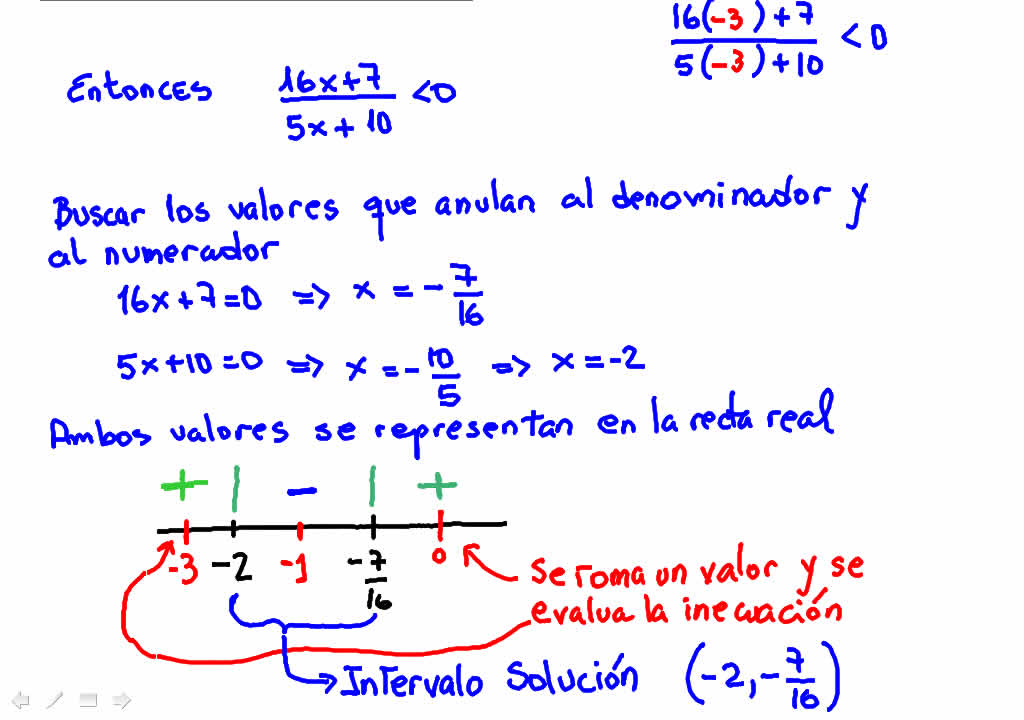
En la segunda imagen ya se observa el estudio, buscando los valores que anulan la fracción en el numerador, para luego representarlo en la recta real.
Para responder la consulta de Wilbert donde solicitan la resolución de un ejercicios (28/02/2014)

Se coloca un vídeo con el ejemplo que solicitas (Nuevo canal de Youtube)
Se responde con un video en el mismo articulo (Nuevo Canal de Youtube)
Se responde con un video en el mismo articulo
Perdon es en el ultimo ejercicio q dice de wilbert.. Entonces ese -2 q esta multiplicando pasaria dividiendk y el simbolo cambiaria a menor igual.. Dando como respuesta: <-00, -3] u .. Porfavor espero su respuesta
Buenas licenciada tengo una consulta. En el 2do ejercicio en el numerador cuando factorizo le qedo.-2(X+3) .. el -2 no pasaria a dividir al 0 del otro lado? y el simbolo de mayor igual no cambiaria a menor igual?
Prof, ¿ tiene algunos ejemplos con la variable al cuadrado y en el denominador? gracias
Gracias por tu comentario
muy buena la forma de orientar matematicas la profe
Hola Profe buen dia necesito su ayuda!!! ¿Como se cuando igualar a 0 una inecuacion racional? ¿Y como resolver una inecuacion cuando la variable esta en el denominador? esta:
3-2/x < 0
Hola Judiht, En una recta real coloca las raíces del denominador y luego prueba con un valor de cada intervalo que se genere. En el primer ejercicio que colocas tienes una sola raíz (1/2), entonces toma un valor a la derecha y otro a la izquierda y evalúas la inecuación con estos dos valores y observa que resultado satisface la desigualad.
Haces el mismo procedimiento con el de abajo, donde tendrás dos raíces, lo que te genera tres intervalos
Buenas noches, no entiendo como realizar estas inecuaciones racionales y ubicar los intervalos en la recta
(X-3)/(2X-1) <0
(2X+3)/((3X-1)*(X+2)) ≥0
Por favor me colaboran, gracias,
Gracias Angela por tu comentario, la función es que los estudiantes vayan consolidando sus conocimientos.
Excelente. Muy buena la explicación. Para los que apenas ven este tema es importante que sepan que toda in ecuacio racional o cuadratica se debe ddes igualar a cero. Y que el sentido de la desigualdad solo cambia cuando se multiplica por un negativo o por el inverso de un negativo.
El dominio del ejercicio donde le intentas aclarar una duda a Wilberth tiene el dominio equivocado, por favor arreglar para evitarnos confusiones a los estudiantes, saludos.
Gracias Rafael por tu comentario. Te puedo dar asesoría para que tengas un sitio educativo. Te escribire a tu correo
HOLA ESTIMADA COLEGA, TU AL IGUAL QUE YO NOS DEDICAMOS A LA ASESORÍA ACADÉMICA, EN MI CASO LO HE ESTADO HACIENDO DESDE HACE 15 AÑOS , BUENO NUNCA EJERCÍ EN EL MINISTERIO YA QUE FUI DISCRIMINADO POR MI CONDICIÓN APOLITICA Y POR PENSAR FUERA DE TODA IDEOLOGIA Y RELIGION POR EL ACTUAL GOBIERNO, PERO SIENTO GRAN SATISFACCION DE HACER DE LA CALLE EL AULA DE CLASE Y LOS ESTUDIANTES DE LAS UNIVERSIDADES MIS PARTICIPANTE, DISCULPA EL DISCURSO YO ME LLAMO RAFAEL QUISIERA SABER COMO HICISTE TU PARA CREAR TU PAGINA WEB QUISIERA PONER A DISPOSICION DE LOS ESTUDIANTE VIDEOS, MATERIAL DIDACTICO DE CALCULO, ALGEBRA, ESTADISTICA, GEOMETRIA , FISICA Y QUIMICA, TE FELICITO TU SITIO ES MUY IDEAL Y ERES MUY SIMPATICA
Hola Rogelio, encontraras de todo un poco y es dificil mantener contento a todos los visitantes. Algunos se quejarán de que los trato como unos lentos y otros que quieren más detalles. Pero si solicitas otra forma con gusto te ayudo
No me gusto, me parece que deberia explicar mejor, o paso por paso para las personas que estamos viendo esto por primera vez…
Muy buena la explicación, me ha servido de mucho.
Quisiera saber la solución de estos ejercicios : x²+x+1÷x(x-1)(x-2)<0 gracias
7x/(3x^2 +11x-20) – 5/(3x+15) ≥ 2x/(6x-8)
no entiendo el segundo ejercicio como determinas las soluciones, y como sabes si se consideran o no
Revisè el 2do. ejercicio y los intervalos soluciòn son: desde -infinito hasta -3 incluìdo, Uniòn intervalo abierto -5/4 ; 1/2.
Revisa el articulo, coloque una imagen con la resolución del ejercicio
necesito su ayuda nose como resolver -1/2x-1_>-1/4x+5
necesito saber que pasa cuando la fraccion se presenta en el otro lado de la desigualdad, este caso lo explica 2x-3=7/(3x+3) que sucede ?? please si pueden conctestar rapido seria genial
Ante todo, buenas noches, mi nombre es Carolina y me dirijo ante este medio con el fin de plantear una inquietud con respecto a las inecuaciones racionales, ¿Cuándo una inecuación es racioonal y su numerador y denominador es negativo se cambia completamente el sentido de la misma? Un ejemplo es -2x+6/-x-1>=0 =>(-1) -2x+6/-x-1 >=o (-1) 2x-6/x-1<=0 raíces (N) x=3 (D)x=1 Sol[1,3] ¿Estaría este procedimiento y resultado correcto? Le agradecería mucha la ayuda que pueda proporcionarme.
MUY BUEN EJERCICIO Y BIEN EXPLICADAO, GRACIAS.