Ecuación lineal con valor absoluto y raíz cuadrada (Ejercicios solicitado por visitante)
Ecuación Lineal con Valor absoluto en el miembro de la izquierda y una raíz cuadrada en el miembro de la derecha.
Cuando se tiene una ecuación lineal, el objetivo es buscar el valor de la variable.
Debe realizar las operaciones conocidas como suma, resta, multiplicación, división, potencia y raíces.
Es importante recordar que los términos son las expresiones que se suman o se restan. Que cuando se pasan a otro miembro sea el de la derecha o izquierda, pasarán con operación contraria.
Que los factores son expresiones que se multiplican o dividen. Que al pasarlo para el otro miembro sea el de la izquierda o derecha pasaran con operación contraria, es decir, si multiplica pasara dividiendo.
Ahora en el ejemplo que estudiamos (el cual fue solicitado por un alumno) se tiene en el miembro de la izquierda un Valor Absoluto. Esto indica que se generan dos ecuaciones.
Recordemos que el valor absoluto por definición establece:
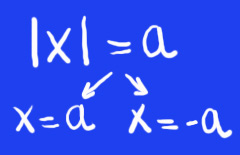
En el miembro de la derecha hay una raíz y como cantidad subradical aparece la variable, por lo tanto se debe considerar que la ecuación se tendrá que elevar al cuadrado para poder eliminar la raíz.
Aclaro que el ejercicio se realiza según lo que se entiende de lo anotado en el comentario.
Al realizar las operaciones pertinentes se obtiene que la ecuación no tiene raíces en los reales.
Se despide
Aprende Matemáticas
Aprender Matematicas online
Estudiar Matematica por Intener
En LaProfeMatematica.com





hola necestio calcular que g(2y)=2√1-y^2 todo esto va en la raiz y teniendo en cuenta que g(y)=√4-y^2 para lxl menor o igual a 2