Medidas de Dispersión, Rango, Varianza y Desviación Estándar
La Dispersión permite analizar cómo se dispersan los valores de una variable de tipo intervalo/razón de menor a mayor y la forma gráfica que estos valores presentan. Si se conoce la media de una población hay distintas posibles formas de distribuir los valores, e posible que todos estén alrededor de la media o podrín estar sesgados hacia un lado. Estudiar la dispersión es revisar el eje horizontal y observar donde están alojados los datos.
Entonces los Estadísticos de Dispersión o Medidas de Dispersión describen como se dispersan los datos de una variable a lo largo de su distribución. Las Medidas de Dispersión son: el Rango, la Desviación Estándar y la Varianza.
El Rango es una Medida de Dispersión que indica cómo los datos de una variable se distribuyen de menor a mayor, es decir la distancia entre el valor mínimo y máximo, es fácil de calcular porque solo deberá restar el valor máximo menos el valor mínimo. El Rango se ve afectado cuando exista valores muy aislados del grupo, la información que suministra no dice nada de la distribución de puntuaciones
La Desviación Estándar es una Medida de Dispersión que describe la forma en que los valores de la variable se dispersan a lo largo de la distribución en relación a la media. El cálculo de la Desviación Estándar involucra cuanta separación existe entre el valor y la media, así como el número de datos, por lo tat es una medida que involucra a todos los datos de la muestra o población.
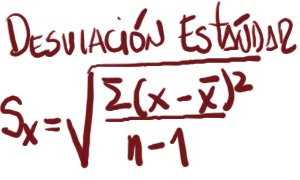
La fórmula de la desviación Estándar involucra un factor denominado Puntuación de desviación el cual indica la cantidad a que la puntuación se aleja de la media y la dirección de la puntuación, si está por arriba o por debajo de la media.
La Varianza se obtiene antes de calcular la raíz cuadrada de la Desviación Estándar, lo que indica que muestra la media de la suma de cuadrados.
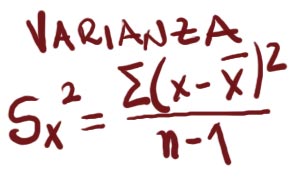
Estas tres medidas se combinan con las de Tendencia Central para permitir un análisis de resultados adecuados.
