Funciones y términos básicos
Términos básicos como: dominio, rango, conjunto de partida, conjunto de llegada…
Una función es una relación entre dos variables que permite obtener el valor numérico de una de las variables una vez conocido el valor numérico de la otra variable.
Existen muchas aspectos de la vida cotidiana donde se aplica el concepto de funciones como por ejemplo el consumo de electricidad diariamente, el consumo de gasolina por kilómetros recorridos, entre otras.
Existen varios términos alrededor de FUNCIÓN, como los son dominio, rango, conjunto de partida, de llegada, variable dependiente, independiente, Diagrama Sagital.
El dominio es el conjunto de valores que satisfacen a la función, es decir que permiten que la función existe, y que representan a la variable independiente. Es el valor de la «x» por lo tanto son los valores del eje horizontal en el plano cartesiano. Coincide con el conjunto de partida.
El Rango es el conjunto de valores numéricos que se obtienen una vez realizadas las operaciones cuando se sustituye la variable independiente. Es el valor de la «y» por lo tanto son los valores del eje vertical en el plano cartesiano. Coincide con el conjunto de llegada.
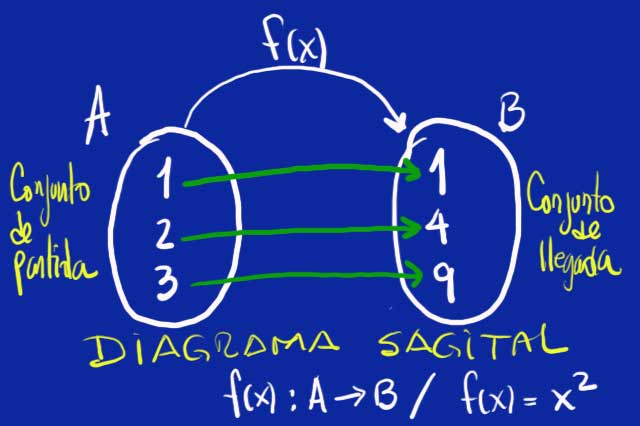
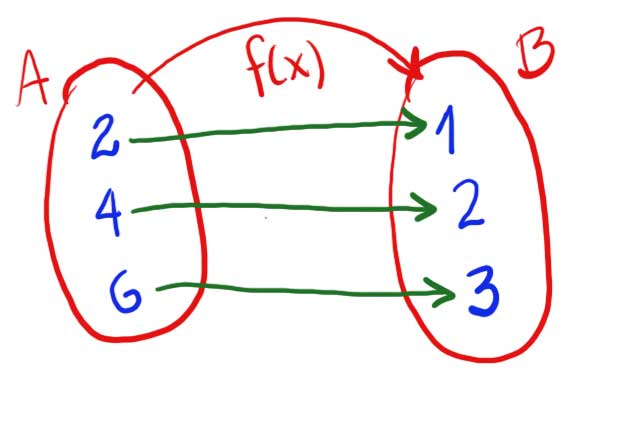
Diagrama Sagital es la representación gráfica de la relación entre dos conjuntos, se observa el conjunto de partida y de llegada y la relación entre sus elementos.
Conjunto relación es donde se representan los pares ordenados de la relación, es decir el par de valores numéricos conformados por el número del conjunto de partida con el número del conjunto de llegada, que están relacionados.
La relación entre los conjuntos se hacen a través de reglas, normas, leyes o ecuaciones que deben cumplir los valores del conjunto de partida y así poder obtener un número que debe estar en el conjunto de llegada.
Es importante que aprendas como identificar una relación y una función. Se puede decir que toda función es una relación, pero no toda relación es función.
A definiciones básicas también es importante que manejes los tipos de funciones como inyectiva, sobreyectiva e inyectiva.
Si estas leyendo este artículo es porque andas buscando consolidar tus conocimientos de una clase presencial. En la actualidad estudiar matemática por Internet es un hecho cada día más común