Concavidad de la funcion Cuadratica

Qué es la concavidad de la funcion cuadratica

La función cuadratica necesita para ser grafica 8 puntos, entre ellos el vértice.

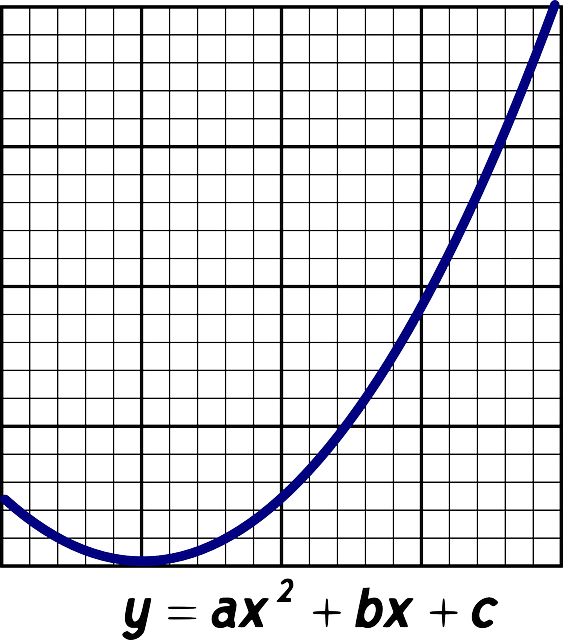
Al graficar una función cuadrática en un plano cartesiano se obtiene una Parábola, la cual puede tener la concavidad hacia arriba o hacia abajo. Para identificar que tipo de concavidad tendrá la función cuadrática, basta con observar el coeficiente del primer término, es decir, el término que tiene la variable elevada al cuadrado.

Si el coeficiente es positivo entonces la concavidad será hacia arriba, en caso contrario la convacidad será hacia abajo.

La función cuadrática se comienza a estudiar en segundo año de Educación Media General, donde se le conoce como Trinomio, se trabaja con el polinomio que representa la función, para encontrar la raíces del mismo, aplicando la factorización.

Luego en Tercer año, se comienza con un repaso de las tres factorizaciones que se le pueden aplicar a un Trinomio, es decir a una ecuación cuadrática. Y se enseña que existe un método que abarca a todas las Factorizaciones que es la aplicación de la «Resolvente«.

Con la resolvente se puede identificar cuando la función cuadrática, corta al eje en dos raíces distintas o iguales, o cuando no corta al eje «x».

Una función cuadrática, a parte de tener corte con el eje «x», tiene un punto llamado vértice que puede ser máximo o mínimo. Se determina sus coordenadas aplicando una fórmula que se deduce de la ecuación general.

La Parábola es también llamada Cónica, entre ellas se encuentra la circunferencia, la hipérbola, la elipse. Las cónicas se producen cuando se hace el corte entre un plano y un cono circular recto.

Las cónicas pueden representar fenómenos naturales y tienen múltiples aplicaciones, entre las cuales se pueden nombrar las órbitas de los planetas, los engranajes elípticos, edificaciones con estructuras particulares que se pueden semejar a las hipérbola.

Así como se conoce que un trimonio representa una parábola, y que analíticamente se puede estudiar el comportamiento de la curva. También teniendo la clasificación de cónicas se pueden obtener ecuaciones generales y particulares, y se establece que definen un lugar geométrico.